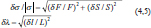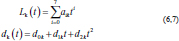| Case Report | ||
Open Vet J. 2022; 12(3): 414-425 Open Veterinary Journal, (2022), Vol. 12(3): 414–425 Case Report Empirical case report of the mechanical properties of three spayed canine lumbar vertebraeErnest Kostenko1*, Rimantas Stonkus2 Jakov Šengaut3 and Algirdas Maknickas11Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius, Lithuania 2Department of Mechatronics and Robotics and Mechanical Engineering, Vilnius Gediminas Technical University, Vilnius, Lithuania 3Private Jakov Veterinary Centre, Vilnius, Lithuania *Corresponding Author: Ernest Kostenko. Department of Biomechanical Engineering, Vilnius Gediminas Technical University, Vilnius, Lithuania. Email: Ernest.kostenko [at] vilniustech.lt Submitted: 13/03/2022 Accepted: 26/05/2022 Published: 25/06/2022 © 2022 Open Veterinary Journal
AbstractBackground: Today, animals, like humans, suffer from spinal illnesses, which are aggravated in old age. Much emphasis is placed on diagnosis and treatment, but little focus is given to the spine’s mechanical properties. Degenerative spine diseases are a major problem throughout the world. According to the World Health Organization, osteoporosis is a world-class public problem that reduces bone mass, resulting in bone fracturing and increased risk of bone fracturing. Therefore, the mechanical investigation of vertebrae can provide more information about the development of osteoporosis.s. Case Description: For our case report, we used spayed mongrel lumbar vertebrae samples obtained from a canine which was about 8 years old and weighed 28 kg. The dog was diagnosed with a mammary tumor, and its owners decided to euthanize the dog. All consent forms were filled. Conclusion: Mechanical tests were performed on three vertebrae, and a notable difference was observed in the first cycle of the first vertebra (L1). Second-order polynomials for displacement and seventh-order polynomials for pressure were proposed for describing the stress–strain relationship of the vertebrae under the cyclical loads. Our research protocol has been broken down into several parts. After measuring the area of the loaded surface, the largest area was in the L2 vertebra (176 ± 16 mm; 177 ± 3 mm) and the smallest was in the L7 vertebra (156 ± 4 mm; 151 ± 33 mm). The smallest distance was recorded between the first (L1) and seventh (L7) lumbar vertebrae (L1) (15.17 ± 0.93 mm), and the largest distance was recorded between the L3 and L4 vertebrae of the lumbar (19.8 ± 3.7 mm). Keywords: Canine, Lumbar, Vertebrae, Osteoporosis, Spine. IntroductionResearchers all around the globe are working hard to develop an appropriate model for the study of bone-induced metabolic disorders, one of which is osteoporosis, which is becoming more common (Turner, 2011). According to a survey of the scientific literature, the subjects of the research are rats, mice, and other small animals housed in vivarium (Banu, 2011), with just a few studies involving bigger animals (such as dogs) being conducted. These animals are merely listed as potential animal models that might be used to investigate the aforementioned osteoporosis (Reinwald and Burr, 2011), but there have been very few studies on them, or when other criteria have been studied, they have been missed. To determine the presence of osteoporosis, it is usual to examine the lumbar vertebrae or long limb bones such as the femur, tibia, or forearm (Reinwald and Burr, 2011), since these are most often fractured in osteoporosis (Reinwald and Burr, 2011). During an experiment in vitro, these bones may be bent or compressed, as well as twisted with a certain amount of force, allowing the mechanical characteristics of the bone to be determined (Markel et al., 1994). Rats are considered the gold standard in the research of postmenopausal osteoporosis (Popović et al., 2016). According to other authors, osteoporosis can be modeled using large animals (e.g., rabbits, dogs, sheep, goats, and pigs) (Sharma et al., 2021). Around 1985, the first mice were bred; their ovaries (which produce the hormone estrogen) were removed in order to mimic the postmenopausal state of osteoporosis (Banu, 2011). In the future, we want to use the accessible biological material to examine other samples. Additionally, we wish to test the concept that the mechanical properties of bone tissue are impacted by a lack of hormones, specifically estrogen. We believe gender influences the mechanical properties of bone tissue. Therefore, small and large animals are useful in studying osteoporosis (Sipos et al., 2014.). Removing the ovaries reduces the size, thickness, and number of trabeculae, which reduces bone density and increases the risk of bone fractures. A significant decrease in bone density in the lumbar spine was observed in rats approximately 2 months after ovarian removal (Banu, 2011). Dogs are also currently being used for osteoporosis research. Researchers mostly use beagles as the breed. Furthermore, dogs are commonly used in biomedical research for their physiological responses (Popović et al., 2016; Sharma et al., 2021). The mature bone composition of dogs is similar to humans, with a similar intracortical remodeling of the Haversian system (Sharma et al., 2021). In dogs, a decrease in bone mass after receiving ovariectomies is observed, especially in the iliac crest (Reinwald and Burr, 2008). Other researchers used beagles to check the bone density of the vertebrae after the dogs received ovariectomies and found that after 8 and 12 months, the bone density of the vertebrae decreased by 8%–10% (Boyce et al., 1990). Historically, dogs, cats, pigs, primates, rodents, guinea pigs, and rabbits have been used to study osteoporosis (Turner, 2001); researchers have long been studying osteoporosis by performing mechanical experiments on various vertebrae in animal spines to identify the perfect animal. Some authors believe that the cervical vertebrae of the sheep, as well as the lumbar vertebrae of the pig, most resemble the vertebrae of humans and are suitable for investigation (WSAVA Animal Welfare Guidelines, 2018). These researchers conducted a study in which they used two static axial forces: an axial compressive force and design and bending. The forces were first applied to intact vertebrae and then using clamps. In a biomechanical test, compression of the vertebrae was analyzed, during which the compressive force was changed with varying displacement. The angular displacement moment was observed in the bending test (WSAVA Animal Welfare Guidelines, 2018). The mechanical properties of bone can be determined by simple tensile or compressive tests. Bouzakis et al. (2004) studied the mechanical properties of the second lumbar vertebra (L2) and later split it into finite elements. According to Turner (2001), long-term studies using beagles have shown an 8%–10% reduction in spinal bone density after neutering. By examining bone density, strength, and structure, some studies describe only a slight decrease in bone density after sterilization (Turner, 2001). Our case report’s objective was to investigate the mechanical characteristics of the first three lumbar vertebrae of a neutered 8-year-old canine female. This information will be used in the subsequent tests to develop a model of the vertebra for future research. Additionally, we advanced a hypothesis in our research in order to verify or deny the concept that the mechanical characteristics of a neutered canine female altered during hypoestrogenism. Case DetailsA necropsy was performed on the animal, during which the lumbar vertebrae from L1 to L7 were separated (Fig. 1a–c). The resulting segment was frozen in a refrigerator at −20°C. The segment obtained in the biomechanical study was gradually thawed to room temperature (22°C). The segment was treated, and the surrounding muscular and fatty connective tissues were separated. Each vertebra was separated, and the spinal cord was removed. Mechanical testFor the present research to be meaningful, it is necessary to understand the basic external forces of compression, bending, and rotation. In living organisms, these forces affect the connective tissue, one of which is bone connective tissue, since they most often act in combination with typical complex deformations. Canids have seven lumbar vertebrae. The shortest transverse processes have the first lumbar vertebrae (L1), and the longest lumbar vertebrae are usually the third (L3) and fourth (L4) in domestic animals (except for dogs, in which the longest transverse process can be found in the fifth (L5) or sixth (L6) lumbar vertebrae) (König and Liebich, 2020). Some costal (rib), caudal articular, and cranial articular processes of the lumbar vertebra were shortened to avoid interference with the compression of the specimen. We tested each lumbar spine vertebra obtained using a Mecmesin MultiTest 2.5-i micro compression machine (Mecmesin Limited, Slinfold, UK). The Mecmesin AFG25 cell-controlled deformation was measured with an accuracy of ±0.01 mm, and the compressive force ranged from 2 to 2,500 N, with an accuracy 100 of ±0.1% and a cross-speed accuracy of ±0.1%. The experiment examined the mechanical qualities of the imprinted 3D model of the lumbar spine using this device (Maknickas et al., 2019). Each vertebra was compressed with 950 N. The selected speed was 1 mm/minute (Fig. 2). The vertebrae were compressed 10 times. After the experiment, the axes of each vertebra were measured. After the specimen was installed, cyclic loading was applied. This machine was also used to measure cyclic loads on porous materials (Porrelli, et al., 2015).
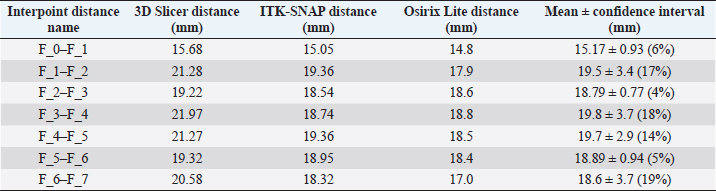
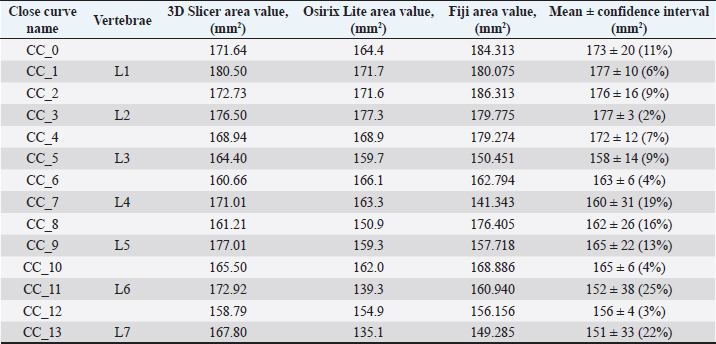
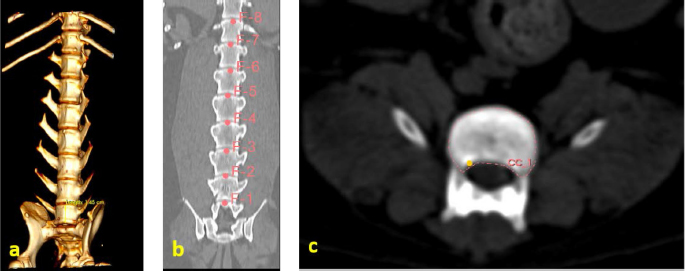
Fig. 1. (a) Canine lumbar caudo-cranial vertebrae view. (b) Canine lumbar latero-lateral vertebrae view. (c) Canine lumbar dorsoventral vertebrae view. Evaluating errorsTwo types of data were used for determining the vertebrae pressure–stretch relationships. The first was vertebra geometry data, which were retrieved directly from CT images of the euthanized dog. The CT images were imported into 3D Slicer v4.13 (Fedorov et al., 2012), ITK-SNAP (Yushkevich et al., 2006) and Osirix Lite (Rosset and Spadola, 2004) for further analysis. To estimate the confidence interval, we used three different software: 3D Slicer, Osirix Lite, and ITK-SNAP. The second type of data was that obtained from the compression machine MultiTest 2.5-i, which were presented as force (measured in N) and displacement (measured in mm). Therefore, we needed geometric data of the vertebrae to evaluate the stress–strain relationships. At first, the lengths of the vertebrae were measured by dropping two markup fiducial points and obtaining the distance between them by switching to the Markups module in 3D Slicer, selecting both fiducial points in the list, and right-clicking in the list. The fiducial points were marked between longitudinal axes of the vertebrae; one assumes the compressions are placed on the rostrocaudal axis of the vertebrae. Later, the surface area of the loading vertebra contact zone was determined by marking the intervertebral zone with a closed curve (CC) and obtaining the surface area of the close curve in the same Markups module of 3D Slicer. The obtained results are presented in Tables 1 and 2. In addition, the confidence intervals of the measured vertebrae lengths and loading surfaces were evaluated using the following expression (King and Eckersley, 2019):
where t is the Student’s coefficient, s is the standard deviation, and n is the degree of freedom plus 1. The Student’s coefficient is 4.303 for two degrees of freedom, in which we chose a confidence interval of 95% (Table 1) (King and Eckersley, 2019). Finally, the propagation of error of the two variable functions for external pressure induced σ stress as
where F is the measured load force and S is the vertebra loading surface (Fig. 3c) and λ stretch is
Fig. 2. Canine lumbar vertebra compression. where L is vertebra length between loading surfaces (Fig. 3a), which can be expressed as follows (Ku, 1966):
Table 1. CT image-based vertebrae length data.
Table 2. CT image-based vertebrae-loading contact surface area data.
Approximation of experimental curvesParametric equations are commonly used to express the coordinates of the points that make up a geometric object, such as a curve, in which case, the equations are collectively called a parametric representation (Thomas and Finney, 1979; Lapshin, 2020). The collected experimental data of the increasing and decreasing pressure Lk (t) and displacement dk (t) of the vertebra can be approximated by using the following parametric expressions:
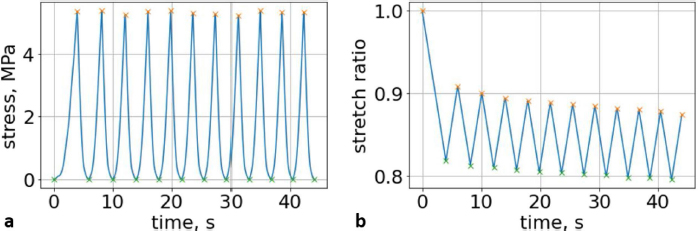
where t is the independent parameter time, and aik and dik are material constants for each load/unload cycle k. The approximation of cyclic curves was performed by second steps. We began by compressing the vertebrae using cyclic loads. We obtained hysteresis loops after compressing the vertebrae 10 times. These obtained cycles are shown in Figure 4. Following that, we determined the minimum and maximum values by analyzing the hysteresis loops. Then, the extreme values of stress and stretch versus time relationships were found. These extreme values were used to determine each compression–relaxation cycle, because each cycle is unique and should be approximated separately (Fig. 5a, b). After that, time indexes of extreme values of obtained stress and stretch array values were approximated by seventh- and second-order polynomials, accordingly. Numerical optimization was applied using the SciPy optimize curve_fit function (Virtanen et al., 2020), and polynomial coefficients were found. All these graphs (Figs. 6–8) were created using a seventh-order polynomial. It is believed that, in living organisms, the hysteresis loop is different due to the compensatory and decompensatory mechanisms involved. Normalization was performed to compare the same mechanical properties of different vertebrae.
Fig. 3. (a) Vertebra length determination in Osirix Lite. (b) Vertebra length determination in 3D Slicer. (c) Vertebra-loading surface area determination.
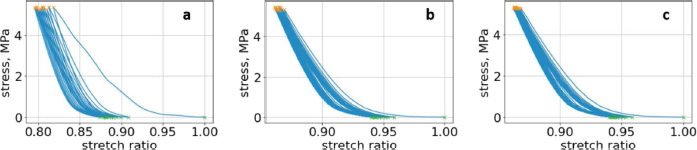
Fig. 4. (a) First lumbar vertebra with all compression cycles, with minimum and maximum values. (b) Second lumbar vertebra with all compression cycles, with minimum and maximum values. (c) Third lumbar vertebra with all compression cycles, with minimum and maximum values.
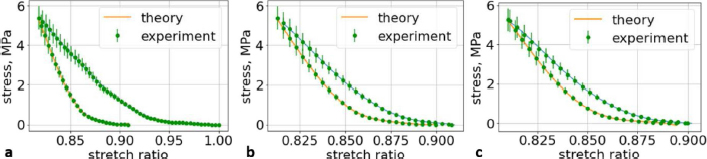
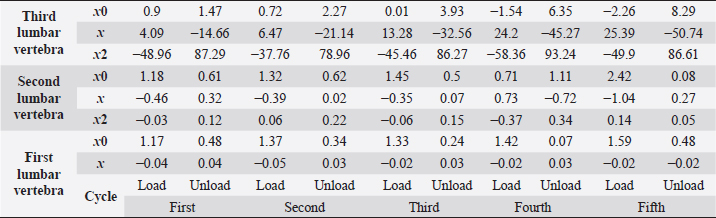
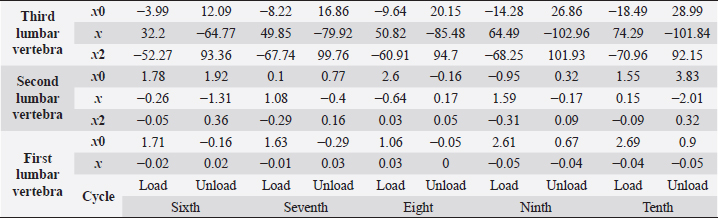
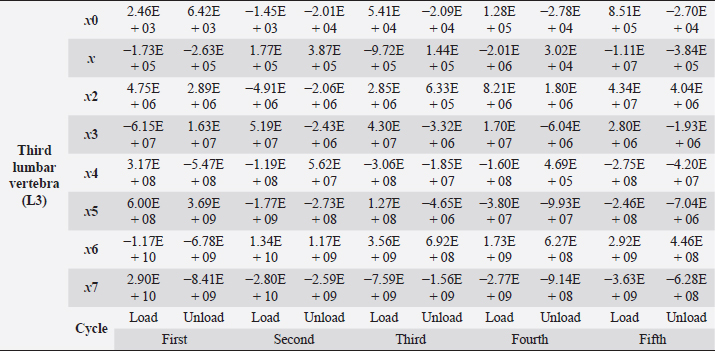
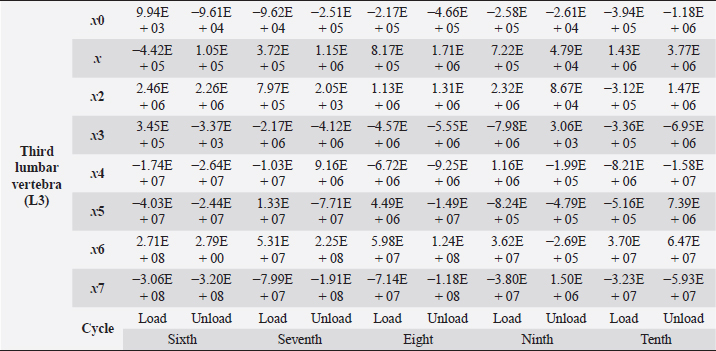
Fig. 5. (a) Extreme values of stress vs time for first vertebra (L1). (b) Extreme values of stretch vs time for first vertebra (L1). The most expressive cycle was the first (Fig. 6a), in which the vertebra adapted to the load acting on it. The second and third cycles show well-defined hysteresis loops, which are comparable to our proposed approximation. Errors of applied load pressure were found and calculated and are displayed on each curve. Many solids form hysteresis loops under pressure, but bone tissue is unique in its properties. In living organisms, when compensatory and decompensatory mechanisms are applied to the bone with higher forces, the bone withstands higher loads. However, it is always necessary to assess the fatigue experienced by the bone. So, in this experiment, we evaluated bone fatigue by applying cyclic loads. The coefficients of the second-order displacement approximation polynomials are given in Table 3, and the coefficients of the seventh-order external load pressure polynomials are given in Tables 4–6. The polynomial coefficients starting from the fourth-degree polynomial terms degraded during the cyclic load. In the first lumbar vertebra, the coefficients for the seventh-order terms went to zero, and those for the sixth-degree reduced hundreds of times. The same coefficients of the second (L2) and third (L3) vertebrae reduced from 10 to 1,000s of times, indicating that dog vertebrae should contain remodeling mechanisms to compensate for the degrading characteristic of the momentum cyclic loads—for example, loads on vertebrae while running. According to our calculations, the L2 vertebra had the largest area (176 ± 16 mm; 177 ± 3 mm), while the L7 vertebra had the smallest area (156 ± 4 mm; 151 ± 33 mm). The shortest distance measured was 15.17 ± 0.93 mm [between the first (L1) and seventh lumbar vertebrae (L7), while the longest distance measured was 19.8 ± 3.7 mm (between the L3 and L4 lumbar vertebrae)].
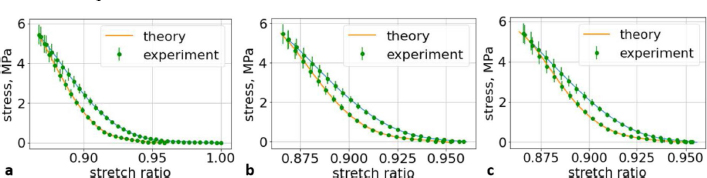
Fig. 6. (a) The first cycle of the first lumbar (L1) vertebra sample. (b) The second cycle of the first lumbar (L1) vertebra sample. (c) The third cycle of the first lumbar (L1) vertebra sample.
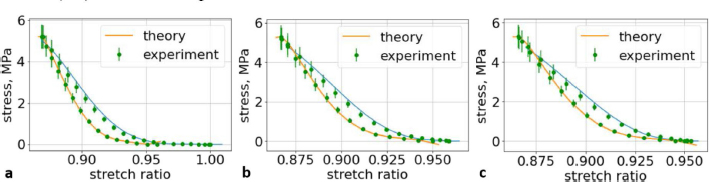
Fig. 7. (a) The first cycle of the second lumbar (L2) vertebra sample. (b) The second cycle of the second lumbar (L2) vertebra sample. (c) The third cycle of the second lumbar (L2) vertebra sample.
Fig. 8. (a) The first cycle of the third lumbar (L3) vertebra sample. (b) The second cycle of the third lumbar (L3) vertebra sample. (c) The third cycle of the third lumbar (L3) vertebra sample. Ethical approvalAll bioethical and animal welfare standards adhered to the Regulation (EC) No 1069/2009 of the European Parliament and of the Council of 21 October 2009 and Regulation (EC) No 1774/2002 (animal byproducts regulation)—17 articles. DiscussionWe understand that a bone tumor can affect the mechanical properties of the bone. In order to check it, it is necessary to take a sample of the bone tissue and examine it at the cytological level, but the owners of the animals refused this. We wanted to evaluate an elderly female dog because we wanted to test the likelihood that animals, like older people, have a tendency to develop osteoporosis, but this has received very little attention in the literature and in practice. Table 3. The coefficients using second-order polynomials.
Table 3. The coefficients using second-order polynomials. (Continued)
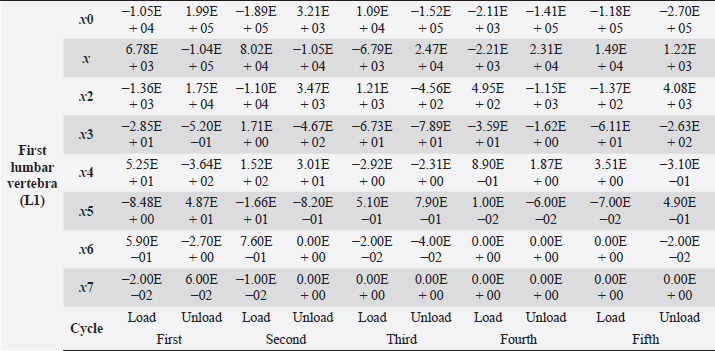
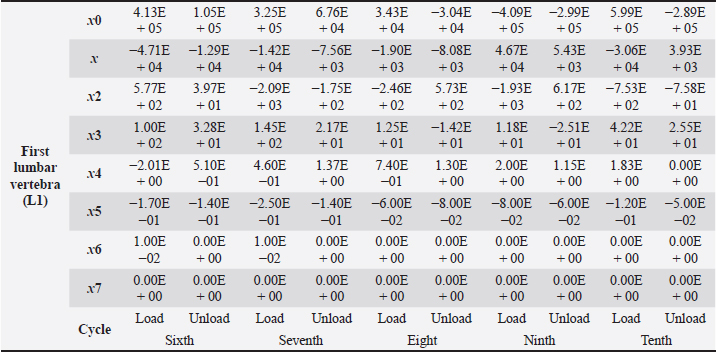
Table 4. First lumbar vertebra coefficients using seventh-order polynomials.
Factors like lack of sunlight, diet, and serum vitamin D levels could change the mechanical properties of the bone as a result of an increased fracture risk factor. Even though we did not look into these risk factors for this case report, we plan to do so for our next article. Table 4. First lumbar vertebra coefficients using seventh-order polynomials. (Continued)
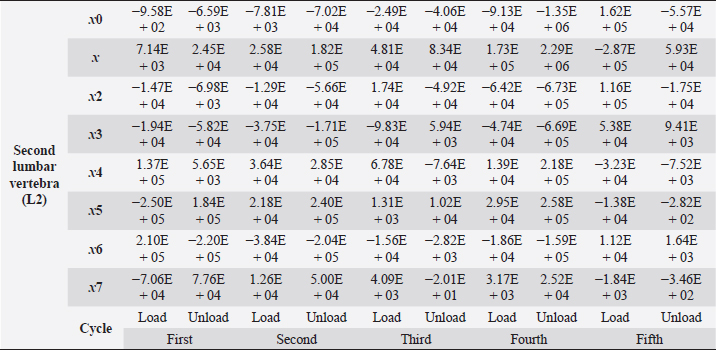
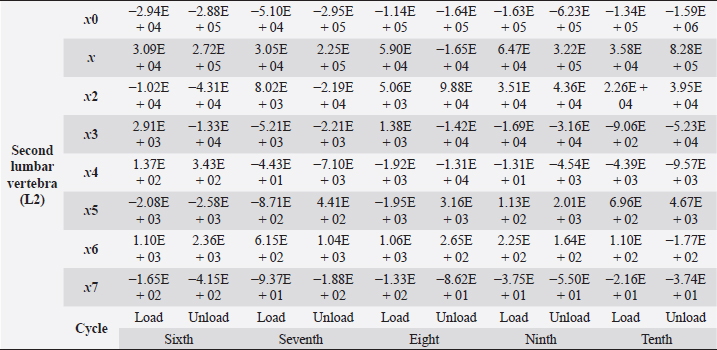
Table 5. Second lumbar vertebra coefficients using seventh-order polynomials.
Factors that alter the bone’s ability to withstand the applied load include eating habits (including food and vitamin D consumption), endocrine hormone status (including age and menstrual status), whether the research object was physically active or had a musculoskeletal disorder and medicines unrelated to bone (including corticosteroids and anticonvulsants) (Bilezikian et al., 2018). We may, however, produce osteoporosis in dogs by reducing the quantity of calcium in their food and performing a hysterectomy on these animals. This was performed by Satoshi Nagai, whose findings in a canine model of osteoporosis may be comparable to the analysis of human osteoporosis. This 30% decrease provides critical information for determining the risk of bone fracture. In the study, 24 weeks after operation (when the BMC of the vertebral cortical bone had decreased by about 20%), the mechanical strength of the femoral neck had decreased. At 36 weeks, BMC had decreased by approximately 30%, and the mechanical strength of the femoral neck had decreased even more markedly. A parallel relationship was observed between the reduction of BMC in the vertebral cortical bone and the reduction of mechanical strength in the femoral neck (Nagai and Shindo, 1997). We know that the dog had been neutered for 2 years and was given a balanced diet on a consistent basis; in addition, no ovarian remnants were discovered after the CT scan. However, we are not going to discuss these factors in this article. We examined the methodology of other authors, in which a lot of attention was paid to sample preparation, with the most attention being paid to the humidity, temperature, and deformation rate of the sample because these factors affect the mechanical properties (Turner and Burr, 2001). Additionally, we selected lumbar vertebrae in our investigation, which were compressed at a rate of 1 mm/minute using a compression machine. We followed the same procedure as previous writers, compressing the lumbar and final thoracic vertebrae at speeds of 1 and 5 mm/minute, respectively (Martin et al., 1987). Table 5. Second lumbar vertebra coefficients using seventh-order polynomials. (Continued)
Table 6. Third lumbar vertebra coefficients using seventh-order polynomials.
In one study, researchers found that, to accurately measure mechanical properties, bone samples should be tested at 37°C; however, this is not always practical. Testing at room temperature increases Young’s modulus of the bone by about 24% compared to testing at 37°C (Bonfield and Li, 1968). The sample was irrigated by constant immersion in physiological saline (NaCl, 0.9%). If this step is ignored, Young’s moduli and bone strength generally increase, but bone toughness decreases. In the human femur, Evans and Lebow showed an increase in Young’s modulus by 17%, an increase in tensile strength by 31% and, after drying the specimen, a decrease in toughness by 55% (Cowin, 2001). Table 6. Third lumbar vertebra coefficients using seventh-order polynomials. (Continued)
While the owner of the animal must ultimately decide whether to castrate it or not, it is worth noting a comprehensive review of the literature that discusses the positive and negative aspects of castration, the methods of castration, and the effect of castration on reproductive function and urinary and musculoskeletal systems. When we sterilize an animal and leave it uncastrated, the most prevalent illnesses are outlined (Urfer and Kaeberlein, 2019). We did not use animals in this research because we value life and believe that there is always an alternative. Instead, we decided to use a dog’s cadaver. The canine was already spayed, which is why we chose her as the object of our case report. Other researchers have conducted many experiments in which they used castrated breeds of female beagles as the subjects of their investigations. For instance, Snow et al. (1984) sought to determine the effect of ovarian hormone deficiency on the activity of cortical bone remodeling in the cortical bone. Additionally, they detected no statistically significant difference in activity between control and spayed females (Snow et al., 1984). We also wanted to test this assumption and this pattern in our research; we effectively disproved our assumption at the conclusion. This has also been proven by Shen et al. (1992) in their study of the effects of several hormones. They studied biochemical indicators such as ionized calcium, parathyroid hormone, osteocalcin, alkaline phosphatase, vitamin D concentration and phosphorus, and found no variation in bone mineral density between castrated females (Shen et al., 1992). Authors’ contributionsThe study was co-authored by all authors. The final manuscript was read and approved by all authors. Conflict of interestThe authors declare that there is no conflict of interest. ReferencesBanu, J. 2011. The ovariectomized mice and rats. In Osteoporosis research. Eds., Duque, G. and Watanabe, K, London, UK: Springer, pp: 101–114; doi:10.1007/978-0-85729-293-3_9. Bilezikian, J.P., Bouillon, R., Clemens, T., Compston, J., Bauer, D.C., Ebeling, P.R., Engelke, K., Goltzman, D., Guise, T., Jan de Beur, S.M., Jüppner, H., Lyons, K., McCauley, L., McClung, M.R., Miller, P.D., Papapoulos, S.E., Roodman, G.D., Rosen, C.J., Seeman, E., Thakker, R.V., Whyte, M.P. and Zaidi, M. 2018. Primer on the metabolic bone diseases and disorders of mineral metabolism, 1st ed. Hoboken, NJ: Wiley. Bonfield, W. and Li, C.H. 1968. The temperature dependence of the deformation of bone. J. Biomech. 1(4), 323–329. Bouzakis, K.D., Mitsi, S., Michailidis, N., Mirisidis, I., Mesomeris, G., Maliaris, G., Korlos, A., Kapetanos, G., Antonarakos, P. and Anagnostidis, K. 2004. Loading simulation of lumbar spine vertebrae during a compression test using the finite elements method and trabecular bone strength properties, determined by means of nanoindentations. J. Musculoskelet. Neuronal. Interact. 4(2), 152–158. Boyce, R.W., Franks, A.F., Jankowsky, M.L., Orcutt, C.M., Piacquadio, A.M., White, J.M. and Bevan, J.A. 1990. Sequential histomorphometric changes in cancellous bone from ovariohysterectomized dogs. J. Bone Miner. Res. 5(9), 947–953. Cowin, S.C. 2001. Bone mechanics handbook, 2nd ed. Boca Raton, FL: CRC Press. Fedorov, A., Beichel, R., Kalpathy-Cramer, J., Finet, J., Fillion-Robin, J.C., Pujol, S., Bauer, C., Jennings, D., Fennessy, F.M., Sonka, M., Buatti, J., Aylward, S.R., Miller, J.V., Pieper, S. and Kikinis, R. 2012. 3D slicer as an image computing platform for the quantitative imaging network. Magn. Reson. Imaging 30(9), 1323–1341. King, A. and Eckersley, R. 2019. Statistics for biomedical engineers and scientists (Kindle). Elsevier Science. König, H.E. and Liebich, H.G. 2020. Veterinary anatomy of domestic animals textbook and colour Atlas, 7th ed. New York, NY: Georg Thieme Verlag. Ku, H.H. 1966. Notes on the use of propagation of error formulas. J. Res. National Bureau Standards 70C(4), 262; doi:10.6028/jres.070c.025. Lapshin, R.V. 2020. An improved parametric model for hysteresis loop approximation. Rev. Sci. Instrum. 91(6), 065106; doi:10.1063/5.0012931. Maknickas, A., Alekna, V., Ardatov, O., Chabarova, O., Zabulionis, D., Tamulaitienė, M. and Kačianauskas, R. 2019. FEM-Based compression fracture risk assessment in osteoporotic lumbar vertebra L1. Appl. Sci. 9, 3013; doi:10.3390/app9153013. Markel, M., Sielman, E., Rapoff, A. and Kohles, S. 1994. Mechanical properties of long bones in dogs. Am. J. Vet. Res. 55, 1178–1183. Martin, R.B., Butcher, R.L., Sherwood, L.L., Buckendahl, P., Boyd, R.D., Farris, D., Sharkey, N. and Dannucci, G. 1987. Effects of ovariectomy in beagle dogs. Bone 8(1), 23–31. Nagai, S. and Shindo, H. 1997. Mechanical strength of bone in canine osteoporosis model: relationship between bone mineral content and bone fragility. J. Orthopaed. Sci. 2(6), 428–433. Popović, T., Šrbić, R., Matavulj, M., Obradović, Z. and Sibinčić, S. 2016. Experimental model of osteoporosis on 14 weeks old ovariectomised rats: biochemical, histological and biomechanical studys. Biologia Serbica 38(1), 18–27. Porrelli, D., Travan, A., Turco, G., Marsich, E., Borgogna, M., Paoletti, S. and Donati, I. 2015. Alginate–hydroxyapatite bone scaffolds with isotropic or anisotropic pore structure: material properties and biological behavior. Macromolecul. Mater. Eng. 300(10), 989–1000. Reinwald, S. and Burr, D. 2008. Review of nonprimate, large animal models for osteoporosis research. J. Bone Miner. Res. 23(9), 1353–1368. Reinwald, S. and Burr, D.B. 2011. Other large animal models. In Osteoporosis research. Eds., Duque, G. and Watanabe, K, London, UK: Springer, pp: 159–174; doi:10.1007/978-0-85729-293-3_13. Rosset, A.R.O. and Spadola, L. 2004. OsiriX: an open-source software for navigating in multidimensional DICOM images. J. Digit. Imaging 17(3), 205–216. Sharma, H., Kumar, A., Sharma, B. and Purwar, N. 2021. Endocrine causes of secondary osteoporosis in adults: mechanisms and evaluation. J. Clin. Diagn. Res. 15(1), OE01–OE07. Shen, V., Dempster, D.W., Birchman, R., Mellish, R.W., Church, E., Kohn, D. and Lindsay, R. 1992. Lack of changes in histomorphometric, bone mass, and biochemical parameters in ovariohysterectomized dogs. Bone 13(4), 311–316. Sipos, W., Föger–Samwald, U. and Pietschmann, P. 2014. Comparative medicine. In Ed., Jensen–Jarolim, E, pp: 87–96. Snow, G.R., Cook, M.A. and Anderson, C. 1984. Oophorectomy and cortical bone remodeling in the beagle. Calcif. Tissue Int. 36(5), 586–590. Thomas, G.B. and Finney, R.L. 1979. Calculus and analytic geometry, 5th ed. Boston, MA: Addison-Wesley. Turner, A.S. 2001. Animal models of osteoporosis–necessity and limitations. Eur. Cell Mater. 1, 66–81. Turner, A.S. 2011. How to select your animal model for osteoporosis research. In Osteoporosis research. Eds., Duque, G. and Watanabe, K, London, UK: Springer, pp: 1–12; doi:10.1007/978-0-85729-293-3_1. Turner, C. and Burr, D. 2001. Bone mechanics handbook, 2nd ed. Boca Raton, FL: CRC Press. Urfer, S.R. and Kaeberlein, M. 2019. Desexing dogs: a review of the current literature. Animals 9(12), 1086; doi:10.3390/ani9121086. Virtanen, P., Gommers, R., Oliphant, T.E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S.J., Brett, M., Wilson, J., Millman, K.J., Mayorov, N., Nelson, A., Jones, E., Kern, R., Larson, E., Carey, C.J., Polat, İ., Feng, Y., Moore, E.W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E.A., Harris, C.R., Archibald, A.M., Ribeiro, A.H., Pedregosa, F., van Mulbregt, P. and SciPy 1.0 Contributors. 2020. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods. 17(3), 261–272. WSAVA Animal Welfare Guidelines. 2018. The World Small Animal Veterinary Association. Yushkevich, P.A., Piven, J., Hazlett, H.C., Smith, R.G., Ho, S., Gee, J. C. and Gerig, G. 2006. User-guided 3D active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage 31(3), 1116–1128. | ||
| How to Cite this Article |
| Pubmed Style Kostenko E, Stonkus R, Šengaut J, Maknickas A, . Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Vet J. 2022; 12(3): 414-425. doi:10.5455/OVJ.2022.v12.i3.16 Web Style Kostenko E, Stonkus R, Šengaut J, Maknickas A, . Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. https://www.openveterinaryjournal.com/?mno=99584 [Access: September 01, 2024]. doi:10.5455/OVJ.2022.v12.i3.16 AMA (American Medical Association) Style Kostenko E, Stonkus R, Šengaut J, Maknickas A, . Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Vet J. 2022; 12(3): 414-425. doi:10.5455/OVJ.2022.v12.i3.16 Vancouver/ICMJE Style Kostenko E, Stonkus R, Šengaut J, Maknickas A, . Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Vet J. (2022), [cited September 01, 2024]; 12(3): 414-425. doi:10.5455/OVJ.2022.v12.i3.16 Harvard Style Kostenko, E., Stonkus, R., Šengaut, J., Maknickas, A. & (2022) Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Vet J, 12 (3), 414-425. doi:10.5455/OVJ.2022.v12.i3.16 Turabian Style Kostenko, Ernest, Rimantas Stonkus, Jakov Šengaut, Algirdas Maknickas, and . 2022. Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Veterinary Journal, 12 (3), 414-425. doi:10.5455/OVJ.2022.v12.i3.16 Chicago Style Kostenko, Ernest, Rimantas Stonkus, Jakov Šengaut, Algirdas Maknickas, and . "Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae." Open Veterinary Journal 12 (2022), 414-425. doi:10.5455/OVJ.2022.v12.i3.16 MLA (The Modern Language Association) Style Kostenko, Ernest, Rimantas Stonkus, Jakov Šengaut, Algirdas Maknickas, and . "Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae." Open Veterinary Journal 12.3 (2022), 414-425. Print. doi:10.5455/OVJ.2022.v12.i3.16 APA (American Psychological Association) Style Kostenko, E., Stonkus, R., Šengaut, J., Maknickas, A. & (2022) Empirical case report of the mechanical properties of three spayed canine lumbar vertebrae. Open Veterinary Journal, 12 (3), 414-425. doi:10.5455/OVJ.2022.v12.i3.16 |